Equações de 2º grau: Saiba como resolver e entenda a Fórmula de Bhaskara

Se a for igual a zero, o que temos é uma equação do 1o grau, logo - para ser uma equação do 2o grau - o coeficiente a não pode ser igual a zero.

a é o coeficiente do termo que possui a incógnita ao quadrado (x2);
b é o coeficiente do termo que possui a incógnita (x);
c é o coeficiente do termo independente.

Na equação - 34a² + 28a - 32 = 0 tem-se:

a = - 34
b = 28
c = - 32

Mas e na equação 10x - 3x² = 32 +15x² ?

Como se viu acima, é possível reduzir a equação à sua forma geral:

Subtraindo 32 de ambos os lados:

10x - 3x² - 32 = 32 +15x² - 32
10x - 3x² - 32 = 15x²

Subtraindo 15x² em ambos os termos:

10x - 3x² - 32 - 15x² = 15x² - 15x²
10x - 3x² - 32 - 15x² = 0

Somando-se os termos em comum:

10x - 32 - 18x² = 0

Colocando em ordem de maior para o menor expoente:

- 18x + 10x - 32 = 0

Agora fica fácil de determinar os coeficientes:

a = -18
b = +10
c = -32

Fórmula geral de resolução de equações de 2° grau

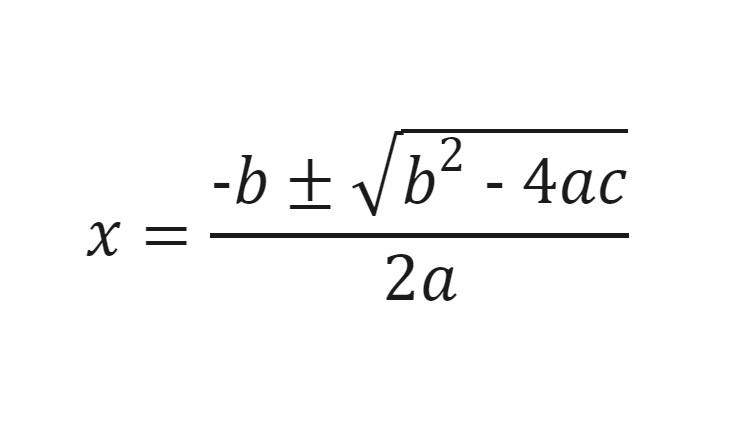
Acima você tem a Fórmula de Bhaskara, utilizada para resolver as equações de 2º grau.

Veja como se chegou até essa fórmula, partindo da fórmula geral das equações de 2º grau:

ax² + bx + c = 0

com a diferente de zero;

Multiplicando ambos os membros por 4a:

4a²x² + 4abx + 4ac = 0;

Somando b² em ambos os membros:

4a²x² + 4abx + 4ac + b² = b²;

Reagrupando:

4a²x² + 4abx + b² = b² - 4ac

O primeiro membro é um trinômio quadrado perfeito (2ax + b)² = b² - 4ac

Tirando a raiz quadrada dos dois membros e colocando a possibilidade de uma raiz negativa e uma positiva ( ± )

: (2ax + b) = ±? b² - 4ac

Isolando a incógnita x

2ax = -b ±? b² - 4ac

Como desde o início a é diferente de zero, essa fórmula nunca será dividida por zero. Ela é conhecida como fórmula de Bhaskara.