Estática - do Corpo Rígido
Estatica do Corpo Rígido
A Estática estuda o equilíbrio dos corpos, ou seja, corpos que estejam parados ou em Movimento Retilíneo Uniforme. Nestes corpos a resultante das forças a eles aplicada é nula. |
Porém, se as dimensões do corpo influírem nos resultados do estudo, um novo componente deve ser acrescentado o momento de uma força. |
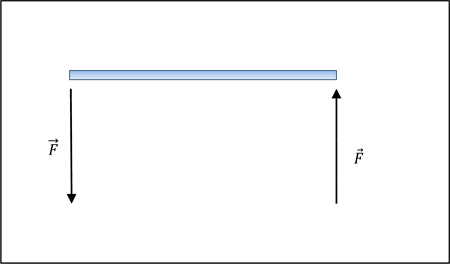
Note que a somatória das forças é nula ( ), mas o corpo se movimenta, pois ele gira. |
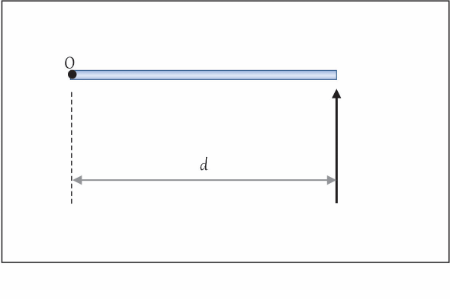
A unidade de medida do momento de uma força é newton.metro (N.m). A distância d será o braço de alavanca, que é sempre medido na perpendicular à direção da força até o seu ponto de aplicação O. |
| Sendo que a somatória das forças pode ser decomposta em duas direções, x e y: |
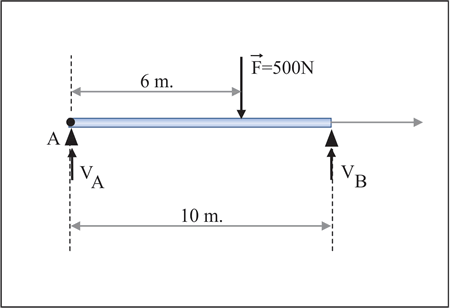
Por exemplo, imagine uma barra biapoiada conforme a figura:
|
| Onde e são as reações de apoio nos pontos A e B respectivamente. Como não há forças na direção horizontal (x), somente serão consideradas forças verticais (y) com o sentido positivo para cima conforme indicado na figura: |
| Adotando-se o sentido horário como positivo e o ponto de giro como sendo A: |
| Substituindo em (I): |








Essa discussão está encerrada
Não é possivel enviar novos comentários.
O autor da mensagem, e não o UOL, é o responsável pelo comentário. Reserve um tempo para ler as Regras de Uso para comentários.